Conjugated Polymer Actuators
Characterization of Behavior of PPy (DBS) Metrics | Inplane Strain | Out-of-Plane Strain | Bilayer Force | Lifetime | Correlation of Strain Color & Current The performance of actuators is judged by “metrics”, such as the main three: strain, stress, and speed. There are also others that are quite important, including efficiency and lifetime, and metrics derived from these previous ones, like power density. The definitions are given here. Engineering Strain The change in length over the initial length, or Engineering Stress The force per unit area, or F/A. Speed The response time, given in either seconds, or as a frequency in Hz. Work Density Work is force x distance, and work density is stress x strain, or work/volume. Efficiency Mechanical work done by the actuator divided by the electrical energy input: W/Ein. Power Density Power is work done in a given time, with power having units of Watts. Lifetime The number of actuation cycles that the actuator can undergo before failure or some given degree of degradation of performance. These are the most important metrics, but there are others that also key, including ultimate tensile strength, hysteresis, and creep. The following table presents some ballpark numbers for the metrics for conjugated polymer actuators. This is not based on a scientific survey of the literature (which is now under way), and these numbers should not be cited or relied upon. This is an area of research that has just recently started receiving attention, so the numbers are not yet well established. Nor do we yet understand how to improve a given metric, but they depend strongly on the polymerization conditions, the polymer, the operating conditions, and any other variable that you would care to name. Since the materials are usually anisotropic (different properties in the plane of the film or along the fiber than perpendicular to that), so are the metrics. Some typical numbers for conjugated polymer actuators.
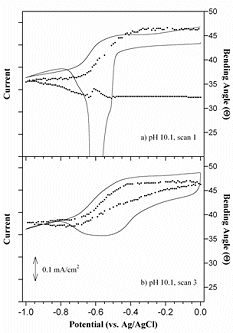
Metrics for Bending Actuators The bending angle is an extrinsic metric, meaning that it depends on bilayer dimensions, like length: the longer the bilayer, the more it curls. To obtain the actuation strain from a bending bilayer, one needs to know the thicknesses of the layers and their Young’s moduli. Then one applies the Timoshenko equation. The actuation strain is not the same as the bending strain. Likewise, the blocked force is extrinsic. The moment is intrinsic. The blocked moment M is the amount of torque required to keep the beam straight when the beam is actuated. The moment is constant throughout the length of the beam. Calculating the moment also requires one to know the thicknesses and moduli of the layers, and the actuation strain. For further information, see the sections below plus: E. Smela, M. Kallenbach, and J. Holdenried, "Electrochemically driven polypyrrole bilayers for moving and positioning bulk micromachined silicon plates," J. Microelectromech. Syst., 8 (4), 373-383 (1999). D. Leo, E. Smela, J. Madden, K. Kim, Z. Ounaies, and D. F. Infante, "Standard testing methods for extensional and bending electroactive polymer actuators," ASME 2005, International Mechanical Engineering Congress and Exposition (IMECE), Orlando, FL, p. 2005-82440 (Nov. 5-11, 2005). B. Shapiro and E. Smela, "Bending actuators with maximum curvature and force and zero interfacial stress," J. Intell. Mater. Syst. Struct., 18 (2), 181-186 (2006). E. Smela, "Conjugated Polymer Actuators," MRS Bulletin (in press) (2008). One might ask, if PPy(DBS) expands during reduction and the film is formed in the oxidized state, why do the microactuators bend up from the surface upon oxidation, rather than backwards, into the wafer, during reduction? It is because the first reduction cycle is anomalous in bilayer microactuators. Although there is a large current, and although the out-of-plane volume increases during the first reduction, there is no bilayer movement, as shown in the figure below. The actuators continue to lie flat. (The figure shows results for meso-scale actuators, but this is also true for microactuators.) Upon re-oxidation, the bilayers curl up, contracting as expected. This means that inplane, the oxidized state during cycling takes up less area than it did after deposition – a permanent molecular re-arrangement takes place during the first reduction. Figure taken from S. Shimoda and E. Smela, "The effect of pH on polymerization and volume change in PPy(DBS)," Electrochim. Acta, 44 (2-3), 219-238 (1998). For further information, see: M. Christophersen, B. Shapiro, and E. Smela, "Characterization and modeling of PPy bilayer microactuators. Part 1: Curvature," S. Shimoda and E. Smela, "The effect of pH on polymerization and volume change in PPy(DBS)," Out of plane strain has been noted by many authors to be larger than inplane strain. We have used AFM and mechanical profilometry to measure the thickness changes in real time and in situ of photolithographically patterned PPy during redox. In PPy(DBS) cycled in NaDBS, the reversible out of plane strain is 35% (as for inplane strain, strain increases during reduction).
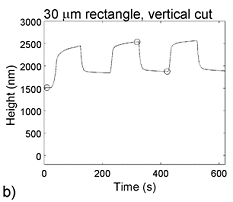
There is, however, also a large one-time increase in volume during the first cycle, which can be seen in the plot. Upon re-oxidation of the film, the thickness does not return to the as-deposited thickness. This is believed to be due primarily to swelling by water, and may have some contribution from molecular rearrangement. For further information, see: E. Smela and N. Gadegaard, "Volume change in polypyrrole studied by atomic force microscopy," J. Phys. Chem. B, 105 (39), 9395-9405 (2001).
Figures taken from Image from E. Smela, M. Kallenbach, and J. Holdenried,
"Electrochemically driven polypyrrole bilayers for moving and positioning bulk micromachined
silicon plates," J. Microelectromech. Syst., 8 (4), 373-383 (1999). The following video shows the movement in the top row of the figure to the right.
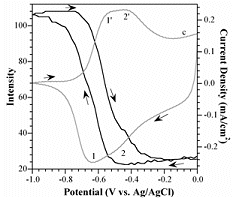
The lifetime of PPy cycled in aqueous solutions is limited because of nucleophilic attack of the polymer backbone. The electroactivity of PPy(DBS) decreases steadily with cycle number in aqueous NaDBS, falling to 50% at 30,000 cycles. In ionic liquids, on the other hand, the lifetime is over a million cycles. For further information, see: "Improving PPy adhesion by surface roughening," Y. Liu, Q. Gan, S. Baig, and E. Smela, "Use of ionic liquids for pi-conjugated polymer electrochemical devices," W. Lu, A. G. Fadeev, B. H. Qi, E. Smela, B. R. Mattes, Correlation of Strain, Color, and Current In PPy(DBS) cycled in NaDBS, there are actually two pairs of peaks. These are particularly well separated in the plot below, the data for which were taken at pH 10 at 1 mV/sec. Bilayer actuation is associated only with the left-most pair of peaks. The same correlation can be seen between changes in the color of the film and the leftmost pair of redox peaks. In the plot below, the intensity of the red channel of a video was recorded during redox, with higher intensity numbers indicating a lighter film (PPy thin films are transparent when reduced, dark red when oxidized, as shown here.)
For further information, see: Plot taken from X. Wang and E. Smela, "Ion transport in conjugated polymers: Part 1. Experimental studies on PPy(DBS)," Good quality PPy(DBS) can be potentiostatically deposited in solutions from acidic to basic up to pH 10. (This is not the case for PPy deposited with mobile anions, which usually cannot be deposited at basic pH.) At pH 11, the film grows in spots. For potentiodynamic polymerization (i.e. deposition by CV), films deposited at pH < 2 are electrochemically inactive, and polymerization at pH 11 is not possible. The pH of the deposition solution affects neither the bending angle nor the actuation speed, so one has flexibility to use whatever conditions produce a good quality film. The pH of the cycling solution does not affect the bending angle, but it does affect the speed. Speed is higher in neutral and basic solutions: at pH 3, the actuators are 4-8 times slower than at pH 7.7 or pH 10.1. PPy(DBS) is electrochemically inactive below pH ~3. For further information, see: S. Shimoda and E. Smela, "The effect of pH on polymerization and volume change in PPy(DBS)," Effect of Salt and Monomer Concentration In PPy(DBS) the so-called “capacitive” current above the oxidation peak is strongly affected by the pyrrole concentration in the deposition solution, as shown in the figure below. In addition, the higher the pyrrole concentration in the deposition solution, the more charge is required to generate the same tip displacement (i.e., a decreased efficiency). Films formed at higher pyrrole concentration were also somewhat slower. Thus, high monomer concentrations should be avoided for actuators.
There is a small effect in the opposite direction for NaDBS concentration, with higher concentrations yielding somewhat larger displacements and somewhat lower charge consumption (higher efficiency). Despite these changes in the cyclic voltammograms, these parameters do not affect the bending angles. CVs and charge consumption between different devices are therefore not predictive of the extent of actuation. For a given device, however, the tip displacement is proportional to the charge consumed. For further information, see: S. Maw, E. Smela, K. Yoshida, and R. B. Stein, "Effects of monomer and electrolyte concentrations on actuation of PPy(DBS) bilayers," Effect of Deposition Current Density
The bending angle of bilayer actuators is inversely correlation with the current density used during electrochemical deposition of PPy(DBS) if voltage is used to control the position. In other words, the higher the voltage/current used during galvanostatic growth of the film, the less the actuators bend, as shown in the plot below. (High voltages during film growth may produce degraded material and/or a greater degree of crosslinking.) When current is used to control the bending, it is proportional to the charge transferred, and the speed increases with the magnitude of the current. For further information, see: S. Maw, E. Smela, K. Yoshida, P. Sommer-Larsen, and R. B. Stein, "The effects of varying deposition current density on bending behaviour in PPy(DBS)-actuated bending beams," Sens. Act. A, 89, 175-184 (2001). Metrics | Inplane Strain | Out-of-Plane Strain | Bilayer Force | Lifetime | Correlation of Strain Color & Current
|
|
|
©2013
 Bilayer actuators rely on inplane strain, which for PPy(DBS) is ~3% (but there is a large
Bilayer actuators rely on inplane strain, which for PPy(DBS) is ~3% (but there is a large 
 Estimates of bilayer force were made by
stacking different glass weights on surface micromachined bilayer actuators and seeing what they could
lift. The hinges were able to lift at least 43,000 times their own weight. The energy: mass ratios
are ~40 mJ/g, and the power density is ~7.5 mW/g
Estimates of bilayer force were made by
stacking different glass weights on surface micromachined bilayer actuators and seeing what they could
lift. The hinges were able to lift at least 43,000 times their own weight. The energy: mass ratios
are ~40 mJ/g, and the power density is ~7.5 mW/g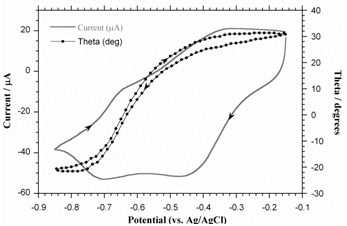
 Plot taken from X. Wang and E. Smela, "Ion transport in conjugated polymers: Part 1. Experimental studies on PPy(DBS)," in preparation (2007).
Plot taken from X. Wang and E. Smela, "Ion transport in conjugated polymers: Part 1. Experimental studies on PPy(DBS)," in preparation (2007).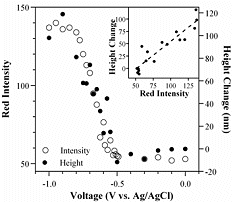 Plot taken from X. Wang and E. Smela, "Ion transport in conjugated polymers: Part 1. Experimental studies on PPy(DBS)," in preparation (2007).
Plot taken from X. Wang and E. Smela, "Ion transport in conjugated polymers: Part 1. Experimental studies on PPy(DBS)," in preparation (2007).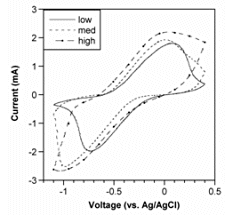 Figure from S. Maw, E. Smela, K. Yoshida, and R. B. Stein, "Effects of monomer and electrolyte concentrations on actuation of PPy(DBS) bilayers," Synth. Met., 155 (1), 18-26 (2005).
Figure from S. Maw, E. Smela, K. Yoshida, and R. B. Stein, "Effects of monomer and electrolyte concentrations on actuation of PPy(DBS) bilayers," Synth. Met., 155 (1), 18-26 (2005).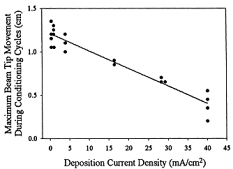 Figure from S. Maw, E. Smela, K. Yoshida, P. Sommer-Larsen, and R. B. Stein, "The effects of varying deposition current density on bending behaviour in PPy(DBS)-actuated bending beams," Sens. Act. A, 89, 175-184 (2001).
Figure from S. Maw, E. Smela, K. Yoshida, P. Sommer-Larsen, and R. B. Stein, "The effects of varying deposition current density on bending behaviour in PPy(DBS)-actuated bending beams," Sens. Act. A, 89, 175-184 (2001).